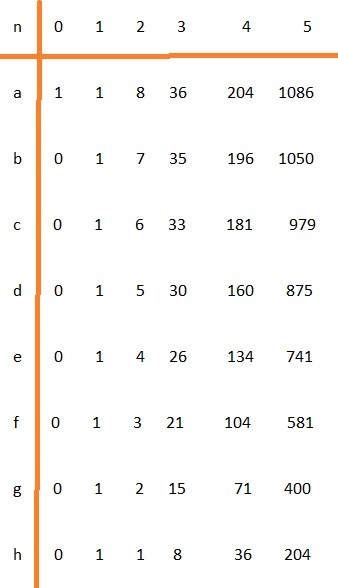
Eighth Order PHI – Fermat's Third Prime: 17
Fermat devised a series of integers based on this formula: 22n + 1, wherein n = {0, 1, 2, 3, 4}. We'll ignore his premise of these being an infinite series of primes, because I'm only interested in their associated series of numbers: 2(2n − 1), wherein n = {0, 1, 2, 3, 4, ...?}. And for the purposes of this webpage, I'll only focus on the third 'n' of n = 2, thereby: 2(22 − 1) = 2(4 − 1) = 23 = 8. The eighth order Golden Series of Numbers and Golden Integers and its associated Golden Polynomial are all embedded within Fermat's third prime for this series, namely: the 17-sided regular polygon, or heptadecagon...
PHI series of numbers, 8th order:
|
a
|
b
|
c
|
d
|
e
|
f
|
g
|
h
|
|---|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
8
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
|
36
|
35
|
33
|
30
|
26
|
21
|
15
|
8
|
|
204
|
196
|
181
|
160
|
134
|
104
|
71
|
36
|
|
1086
|
1050
|
979
|
875
|
741
|
581
|
400
|
204
|
|
5916
|
5712
|
5312
|
4731
|
3990
|
3115
|
2136
|
1086
|
|
31998
|
30912
|
28776
|
25661
|
21671
|
16940
|
11628
|
5916
|
|
173502
|
167586
|
155958
|
139018
|
117347
|
91686
|
62910
|
31998
|
|
940005
|
908007
|
845097
|
753411
|
636064
|
497046
|
341088
|
173502
|
|
5094220
|
4920718
|
4579630
|
4082584
|
3446520
|
2693109
|
1848012
|
940005
|
|
27604798
|
26664793
|
24816781
|
22123672
|
18677152
|
14594568
|
10014938
|
5094220
|
|
149590922
|
144496702
|
134481764
|
119887196
|
101210044
|
79086372
|
54269591
|
27604798
|
|
810627389
|
783022591
|
728753000
|
649666628
|
548456584
|
428569388
|
294087624
|
149590922
|
|
4392774126
|
4243183204
|
3949095580
|
3520526192
|
2972069608
|
2322402980
|
1593649980
|
810627389
|
|
23804329059
|
22993701670
|
21400051690
|
19077648710
|
16105579102
|
12585052910
|
8635957330
|
4392774126
|
|
128995094597
|
124602320471
|
115966363141
|
103381310231
|
87275731129
|
68198082419
|
46798030729
|
23804329059
|
|
699021261776
|
675216932717
|
628418901988
|
560220819569
|
472945088440
|
369563778209
|
253597415068
|
128995094597
|
|
3787979292364
|
3658984197767
|
3405386782699
|
3035823004490
|
2562877916050
|
2002657096481
|
1374238194493
|
699021261776
|
|
20526967746120
|
19827946484344
|
18453708289851
|
16451051193370
|
13888173277320
|
10852350272830
|
7446963490131
|
3787979292364
|
|
111235140046330
|
107447160753966
|
100000197263835
|
89147846991005
|
75259673713685
|
58808622520315
|
40354914230464
|
20526967746120
|
|
602780523265720
|
582253555519600
|
541898641289136
|
483090018768821
|
407830345055136
|
318682498064131
|
218682300800296
|
111235140046330
|
|
3266453022809170
|
3155217882762840
|
2936535581962544
|
2617853083898413
|
2210022738843277
|
1726932720074456
|
1185034078785320
|
602780523265720
|
|
17700829632401740
|
17098049109136020
|
15913015030350700
|
14186082310276244
|
11976059571432967
|
9358206487534554
|
6421670905572010
|
3266453022809170
|
|
95920366069513405
|
92653913046704235
|
86232242141132225
|
76874035653597671
|
64897976082164704
|
50711893771888460
|
34798878741537760
|
17700829632401740
|
|
519790135138940200
|
502089305506538460
|
467290426765000700
|
416578532993112240
|
351680556910947536
|
274806521257349865
|
188574279116217640
|
95920366069513405
|
|
2816730123757620046
|
2720809757688106641
|
2532235478571889001
|
2257428957314539136
|
1905748400403591600
|
1489169867410479360
|
1021879440645478660
|
519790135138940200
|
After 26 iterations, the approximation of the eight roots of the 8th order of PHI accurate to eleven decimal places are...
X1 = a/h = 2816730123757620046 ÷ 519790135138940200 = 5.4189757237403
X2 = b/f = 2720809757688106641 ÷ 1489169867410479360 = 1.8270647407198
X3 = c/d = 2532235478571889001 ÷ 2257428957314539136 = 1.1217342943914
X4 = d/b = 2257428957314539136 ÷ 2720809757688106641 = 0.82969011373757
X5 = e/a = 1905748400403591600 ÷ 2816730123757620046 = 0.67658182242225
X6 = f/c = 1489169867410479360 ÷ 2532235478571889001 = 0.58808506555256
X7 = g/e = 1021879440645478660 ÷ 1905748400403591600 = 0.53620899822299
X8 = h/g = 519790135138940200 ÷ 1021879440645478660 = 0.50866091875829
Return to browsing this file's directory...