• Draw a square.
• With a compass open to an amount equal to half a diagonal of the square, swing an arc with center at a corner of the square, passing through the center of the square and cutting two sides of the square.
• Repeat for the other three corners of the square.
• Through the eight points of intersection of the arcs and the sides of the square, draw four verticals and four horizontals.
• The center square formed by this construction is called the sacred cut square.
• Connecting the eight points of intersection of the arcs and the sides of the square consecutively forms an octagon.

        I did a search for more results up to and including prime 29 which forms the basis of a regular polygon of 166 sides (four times 29), but only found solutions up to the regular icosagon (a polygon with 20 equal sides and angles). The search took 40 minutes using this perl program. The following are its results limited to the: octagon, dodecagon, and icosagon.

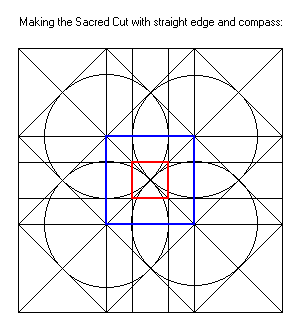
        A "sacred cut" is herein defined as taking the proportions of the sides of two regular squares. These squares are marked off by dissecting diagonals within and (by extension) outside of a regular polygon. The polygon has four times some prime of: 2, 3, or 5, number of sides. So, only 8, 12, and 20 sided polygons will inscribe sacred, squared cuts within themselves (so far as I know; I have yet to do a more thorough search for higher primes; if any were to be found, then a quickie-formula and method could most likely be derived from the data to generate all known cases of sacred, square-cuts to infinity; at least this has been the case with golden ratios and polynomials, but may not exist for sacred, cut squares).

Angle No.1, Sin (45° ÷ 2) = 0.76536686473018 ÷ 2
This means:
The sine of one half of 45° is taken to produce one half of a diagonal within this polygon (an octagon in this case) which is opposite an angle poised at the center of the polygon. So, the sine of 45/2°, or 22.5°, is equal to one half of 0.76536686473018, or: 0.38268343236509. The full value of 0.76536686473018 is used to find the roots of a quadratic polynomial whose coefficients are all real integers. This length is a value relative to the length of the radius of a circle passing through the vertices of this polygon. Proportions are found by dividing one diagonal by another, and by pairing the correct proportions together to form irrational (but real) roots of a polynomial with integer coefficients.

Angles [1^- 3, 1 3^-] Roots {+ 2.41421356237309, – 0.414213562373095} = x² – 2x – 1
This means:
The first of two roots, 2.41421356237309, uses the first and third diagonals associated with the first and third angles, 45° and 135°. 1^- means that 0.76536686473018 (the first and smallest of the three diagonals of an octagon) was raised to the negative power of 1 to create its reciprocal value of 1/0.76536686473018, or: 1.30656296487637. This was then multiplied by the length of the third diagonal, 1.84775906502257, to produce the proportion: 2.41421356237309. The second root, 0.414213562373095, is signed negative in this example. These two proportions: + 2.41421356237309 and – 0.414213562373095 are the roots of the quadratic: x² – 2x – 1. This could be called the Pell quadratic, because the Pell series of numbers (0, 1, 2, 5, 12, 29, 70, ...) can produce these roots. If you divide each number of the series by its immediate neighbor, one of these two roots will be approximated. The extinct planet Maldek used the Pell proportion as its "aesthetic theme". An asteroid belt is all that is left of Maldek between the orbits of Mars and Jupiter.

        Because memories, habits, and personal taste for aesthetics die hard, those of us who hail from Maldek since its demise can relish the proportion inherent within the Pell series. But those of us who are indigenous to Earth may only appreciate the proportion of the golden ratio, since that is Earth's aesthetic theme. The peoples of the more advanced nations of the Earth are mostly populated with Maldekan refugees, while the bulk of humanity is native to Earth. Maldek was a smaller planet with respect to Earth and with a smaller population. When it broke apart, there were no immediate survivors. All the souls of Maldek perished and most were reincarnated, firstly on Earth's moon, and then into the Earth. But this was many aeons ago --- too ancient a memory to get too detailed about. But the legacy remains: a small group of Earth's population require a dual means of finding satisfaction in all things aesthetic, whether it be: astrology, music and art, geometry and architecture, social endeavors, emotions, salts, chakras, Sanskrit letters, energy vibrations, etc. This dual pleasure succumbs to both the Pell and Golden ratios. This is why both ratios were popular during the Renaissance. Roman culture had a particular fondness for the octagon's Pell ratio and any other relationships generated from the square. They used them extensively.

The * symbol will herein refer to "multiplication".
 

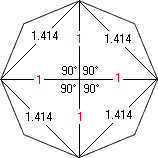
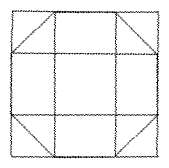
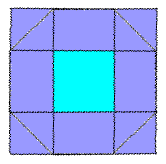
Prime[2] times Square[4] produces an 8-Sided Octagon:

Angular degrees at center of circle with diagonal lengths proportioned to one-half of the longest (central) diagonal of 2 units length:
            Angle No.1, Sin (45° ÷ 2) = 0.76536686473018 ÷ 2
            Angle No.2, Sin (90° ÷ 2) = 1.41421356237309 ÷ 2
            Angle No.3, Sin (135° ÷ 2) = 1.84775906502257 ÷ 2
            Angle No.4, Sin (180° ÷ 2) = 2 ÷ 2

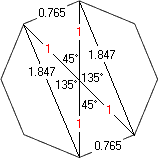
Roots of polynomial derived from selected proportions of diagonals:
            Angle No.s: [1^- * 3, 1 * 3^-] = [3 / 1, 1 / 3] = [1.8477 ÷ 0.7653, 0.7653 ÷ 1.8477] = [2.4142, 0.4142]
            Roots {± 2.41421356237309, 0.414213562373095} = x² 2x – 1 (Polynomial)
 

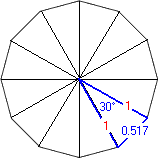
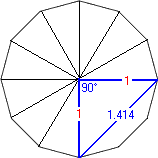
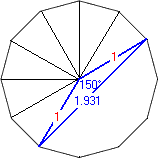
Prime[3] times Square[4] produces a 12-Sided Dodecagon:

Angular degrees at center of circle with diagonal lengths proportioned to one-half of the longest (central) diagonal of 2 units length:
            Angle No.1, Sin (30° ÷ 2) = 0.517638090205041 ÷ 2
            Angle No.2, Sin (60° ÷ 2) = 1 ÷ 2
            Angle No.3, Sin (90° ÷ 2) = 1.41421356237309 ÷ 2
            Angle No.4, Sin (120° ÷ 2) = 1.73205080756888 ÷ 2
            Angle No.5, Sin (150° ÷ 2) = 1.93185165257814 ÷ 2
            Angle No.6, Sin (180° ÷ 2) = 2 ÷ 2

Roots of polynomials derived from selected proportions of diagonals:
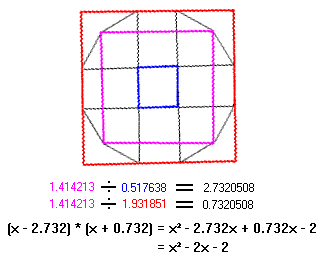
            Angle No.s [1^- * 3, 3 * 5^-] [3 / 1, 3 / 5] = [1.4142 ÷ 0.5176, 1.4142 ÷ 1.9318] = [2.7320, 0.7320]
            Roots {± 2.73205080756888, 0.732050807568877} = x² 2x – 2 (1^st Polynomial)

We will ignore this next case --- a proportional duplicate of the previous, since in the world of ratios, it doesn't matter which diagonal serves as the numerator and which the denominator, but is the resulting proportion unique?:
            Angles [1 * 3^-, 3^- * 5] [1 / 3, 5 / 3] = [0.5176 ÷ 1.4142, 1.9318 ÷ 1.4142] = [0.3660, 1.3660]
            Roots {± 0.366025403784439, 1.36602540378444} = 2x² ± 2x – 1 (Proportional Duplicate of 1^st Polynomial)

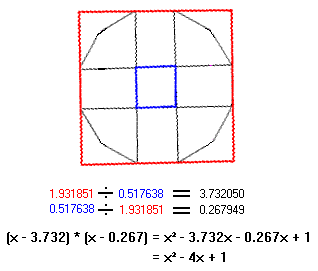
            Angles [1^- * 5, 1 * 5^-] = [5 / 1, 1 / 5] = [1.9318 ÷ 0.5176, 0.5176 ÷ 1.9318] = [3.7320, 0.2679]
            Roots {± 3.73205080756888, ± 0.267949192431123} = x² 4x + 1 (Proportionally Unique 2^nd Polynomial)

Angular degrees at center of circle with diagonal lengths proportioned to one-half of the longest (central) diagonal of 2 units length:
            Angle No.1, Sin (18° / 2) = 0.312868930080462 / 2
            Angle No.2, Sin (36° / 2) = 0.618033988749895 / 2
            Angle No.3, Sin (54° / 2) = 0.907980999479094 / 2
            Angle No.4, Sin (72° / 2) = 1.17557050458495 / 2
            Angle No.5, Sin (90° / 2) = 1.41421356237309 / 2
            Angle No.6, Sin (108° / 2) = 1.61803398874989 / 2
            Angle No.7, Sin (126° / 2) = 1.78201304837674 / 2
            Angle No.8, Sin (144° / 2) = 1.90211303259031 / 2
            Angle No.9, Sin (162° / 2) = 1.97537668119028 / 2
            Angle No.10, Sin (180° / 2) = 2 / 2

Roots of polynomials derived from selected proportions of diagonals:
            Angles [2^- * 6, 2 * 6^-] Roots {+ 2.61803398874989, + 0.381966011250105} = x² – 3x + 1
            Angles [2 * 6^-, 2^- * 6] Roots {+ 0.381966011250105, + 2.61803398874989} = x² – 3x + 1
            Angles [2^- * 10, 6^- * 10] Roots {+ 3.23606797749979, – 1.23606797749979} = x² – 2x – 4
            Angles [2 * 10^-, 6 * 10^-] Roots {+ 0.309016994374947, – 0.809016994374947} = 4x² + 2x – 1
            Angles [4^- * 8, 4 * 8^-] Roots {+ 1.61803398874989, – 0.618033988749895} = x² – x – 1
            Angles [4 * 8^-, 4^- * 8] Roots {+ 0.618033988749895, – 1.61803398874989} = x² + x – 1
            Angles [6^- * 10, 2^- * 10] Roots {+ 1.23606797749979, – 3.23606797749979} = x² + 2x – 4
            Angles [6 * 10^-, 2 * 10^-] Roots {+ 0.809016994374947, – 0.309016994374947} = 4x² + 2x – 1

        Notice that the roots of our Earth-bound, golden, quadratic (the golden mean) is also considered to be square cuts within an icosagon.

Next Lesson: The Sacred Cuts of the Triangle.-->
 
 
Next Lesson: What is the simplest way of generating any series of Golden Numbers?
 
Bibliography:

Watts, Carol Martin & Donald J.: "The Role of Monuments in the Geometrical Ordering of the Roman Master Plan of Gerasa", in Journal of the Society of Architectural Historians, vol. LI (1992): pp.306-314

 

Planetary Anthropology
GCD || Beauty || Concept || Averaging || Comment || Odd || Fermat || Squares || GoldNo.s || Light || Honeybee || Rabbits || Salt || Glossary || Bibliography || BBS

 

My Personal Pages
Book || Topics || Sanskrit || Essays || Poetry || Posts || Links
MyWare || Music || Images || Site Map || References || Home

"> Deutsch Español Français Italiano Português or, Search Here Using....
"> "> &hl=en&lr=&ie=UTF-8&as_qdr=all">Advanced
"> &wf%5B0%5D%5Bw%5D=url.host%3A">Advanced

Home, Sweet Home	Short-Cuts to Sections within Personal Site Map
	Book || Topics || Sanskrit || Essays || Poetry || Posts || Links || Software || Music || Images

"> Deutsch Español Français Italiano Português or, Search Here Using....
"> &wf%5B0%5D%5Bw%5D=url.all%3A">Advanced
"> "> &hl=en&lr=&ie=UTF-8&as_qdr=all">Advanced

">http://